OpTaliX设计系统的优化要求一个高度非线性问题的解决方法。它一个通过改变所选透镜的数据来达到透镜像差最小化的过程(变量)。两种优化算法都可用。
KT-优化,误差函数的最小化通过阻尼最小平方法,解决约束使用的拉格朗日乘数器和塔克优化条件的程序来实现的。
LM-优化使用跨算法解决问题。<br><br>
价值函数通过一些性能和建造数据相关指令构成,因而允许误差函数的定义有无限的灵活性(也可称为价值函数)。另外最小化,边界约束也遵循逻辑运算符。例如<br><br>
= (等于),<br><br>
< (小于)<br><br>
> (大于)<br><br>
用户定义变量和函数也允许更广范围内约束条件的优化,例如<br><br>
$z = [efl]+23.12<br><br>
@xyz == [thi s2]+[thi s4]+$z<br><br>
@xyz > 10<br><br>
定义优化变量,目标,约束
<br><br>
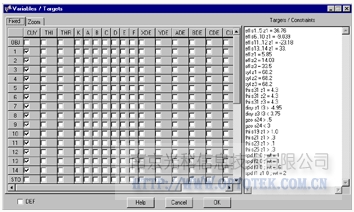
在一个单独的窗口中有编辑变量,目标和约束。用户定义价值函数接受所有的有关球面数据、系统数据和性能数据的指令。这包含数据表达式,一大批内置的数学函数,镜头数据库项目也可以作为宏示例显示:<br><br>
<table cellspacing="0" cellpadding="0">
<tr>
<td valign="top">efl = 100</td>
<td>焦距小于100mm. </td>
</tr>
<tr>
<td valign="top">syl < 70</td>
<td>约束系统波长(第一个表面到最后一个表面)应小于70mm
</td>
</tr>
<tr>
<td valign="top" width="200">spd f1..3 w3..4 0</td>
<td>最小rms-点直径的范围为1到3;波长范围为3到4(目标是0)</td>
</tr>
<tr>
<td valign="top" width="200">spd 0</td>
<td>见上图,最小化rms斑直径。如果没有范围和波长限定,所有的范围和波长都可以。这是最简单的
却具有强大的优化目标</td>
</tr>
<tr>
<td valign="top">thi s1 = [OAL] - 2*[thi s4]</td>
<td> 鉴于括号中使用的算术运算符和透镜数据库项目去定义合成的对象
</td>
</tr>
<tr>
<td valign="top">bfl = sqrt(tan(2)) </td>
<td>使用内部函数定义复杂的目标 </td>
</tr>
<tr>
<td valign="top">@myfkn == [oal s1..6]-5.0 </td>
<td>构建一个用户自定义函数供日后使用
</td>
</tr>
<tr>
<td valign="top">@myfkn > 10 </td>
<td> 使用先前定义的函数去定义约束的优化 </td>
</tr>
</table>

