引言
在激光系统中,如果使用的激光模式较好且发散角较小,在光路设计中我们通常以平行光来代替激光。
使用几何光路设计激光系统的传播。注意:有关激光衍射或自相干除外。
那么下面我们来讨论平行光经过单个平凸透镜聚焦的情况:
首先,我们作一个假设,即这个平凸透镜焦距为定值,此时分为两处情况:球面凸与非球面凸。
对于球面聚焦从像差理论分析,单透镜三阶球差占主导地位。
如果平行光进入的是平凸透镜,即光垂直入射到平面再从凸面传出。
此时我们知道,系统的所有球差必定全部是由后表面(凸面)提供,那么我们在优化时仅仅后凸面起到像差校正的作用。
看实际例子,焦距40的平凸镜,优化后RMS光斑为64um。如下图:
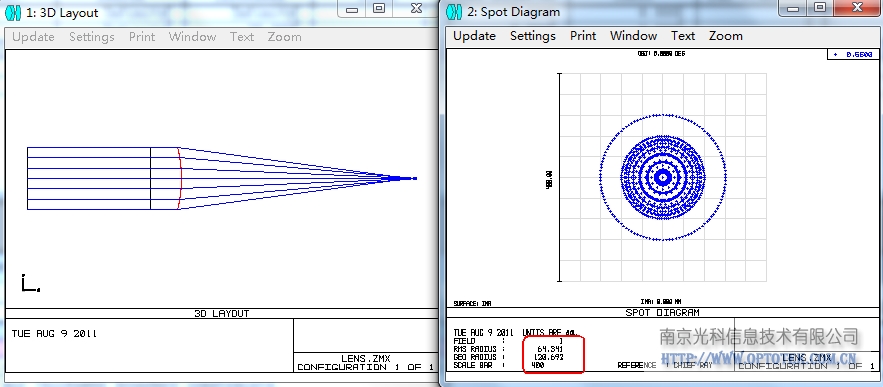
此时的像差贡献如下,从下图中也可以直接看出,所有球差贡献都来自于凸面,前平面不提供任何像差:
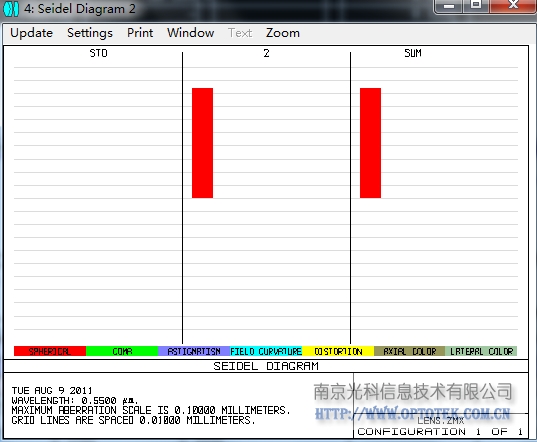
【热点推荐】CAXCAD 光学设计软件
CAXCAD 光学设计软件,包含真实光线追迹,多种面型,几何像差,波像差,衍射PSF MFT, 参数求解,坐标断点,多重结构,DLS 优化等.
CAXCAD 技术知识库正式上线 http://www.caxcad.com/cn/kb.html
下面我们讨论凸平形式,同样从像差理论分析,平行光先经过前表面凸面折射后传播至后表面平面。
此时入射到后表面的光线就不再是垂直入射,这种情况下平面是有像差校正作用的。
如下图,反转过来以后RMS光斑减为15um:
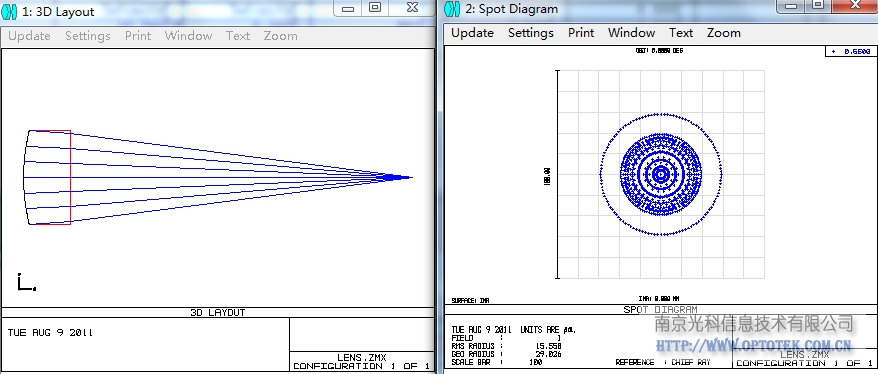
另外从赛德尔像差统计图上也可以看出后平面的像差贡献:
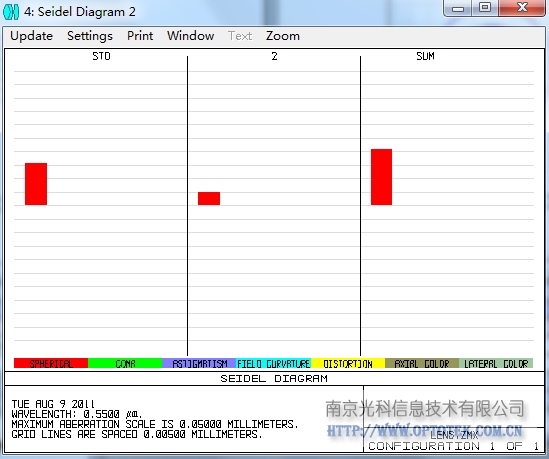
以上是对球面聚焦时平凸与凸平透镜讨论,不难看出,凸平透镜在聚焦光斑上有更大的优势。
以于非球面单透镜聚焦来说,结论则刚好相反,因为非球面可将球差校正为0,也就是说单个球面产生球差时我们使用单个非球面就可以完全校正。
如果非球面处于前表面迎光,则后表面平面则会贡献额外的球差。
前表面Conic非球面时,得到结论如下,RMS光斑大小为0.015:
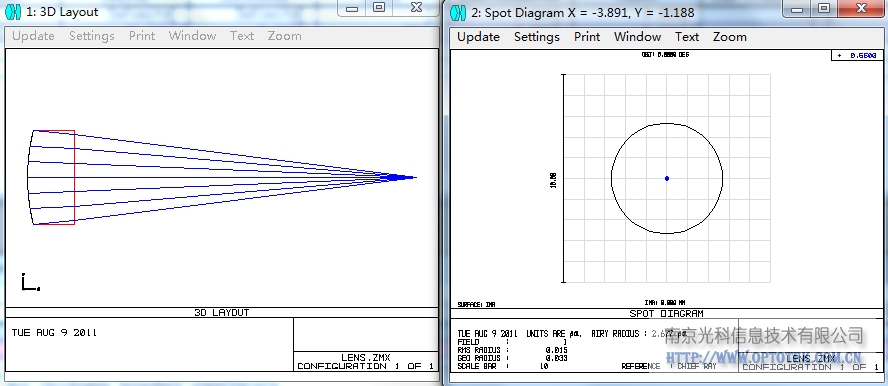
后表面Conic非球面是,得到结论如下,RMS光斑大小为0:

本文详细讨论了不同的球面透镜的像差分析
使用ZEMAX软件给出分析的结果
更多信息,欢迎和我们联系: 
[pagewrap=Footer_Knowledge_ZEMAX_CN.html]